【纯转载】Transformer 中的 positional embedding

原文

关于 positional embedding 的一些问题

重新整理自 Amirhossein Kazemnejad's Blog 。

---

什么是positional embedding？为什么需要它？

位置和顺序对于一些任务十分重要，例如理解一个句子、一段视频。位置和顺序定义了句子的语法、视频的构成，它们是句子和视频语义的一部分。循环神经网络RNN本质上考虑到了句子中单词的顺序。因为RNN以顺序的方式逐字逐句地解析一个句子，这将把单词的顺序整合到RNN中。

Transformer使用MHSA(Multi-Head Self-Attention)，从而避免使用了RNN的递归方法，加快了训练时间，同时，它可以捕获句子中的长依赖关系，能够应对更长的输入。

当句子中的每个单词同时经过Transformer的Encoder/Decoder堆栈时，模型本身对于每个单词没有任何位置/顺序感 (permutation invariance)。 因此，仍然需要一种方法来将单词的顺序信息融入到模型中。

为了使模型能够感知到输入的顺序，可以给每个单词添加有关其在句子中位置的信息，这样的信息就是位置编码(positional embedding, PE)。

---

如何设计positional embedding？有什么规则？

一般我们可能想到的方案是：

1. 给每一个时间步设定[0,1]范围的一个值，0表示第一个，1表示最后一个。这样做的问题是，我们不确定句子里有多少个单词，不同单词数的句子中相邻单词之间的距离就不固定了。
2. 给每一个时间步分配一个数值，例如第一个单词分配“1”，第二个单词分配“2”等等。这样做的问题是，这些值很大，并且实际中遇到的句子可能比训练时见过的句子还要长，这就会导致模型泛化性能变差。

理想情况下PE的设计应该遵循这几个条件：

1. 为每个时间步（单词在句子中的位置）输出唯一的编码；
2. 即便句子长度不一，句子中两个时间步之间的距离应该是“恒定”的；
3. 模型可以轻易泛化到更长的句子上；
4. PE必须是确定的。

---

Attention is all you need中固定类型的PE为什么是这样设计（ sin, cos ）的？

作者设计的这种位置编码的方式非常巧妙。

首先，它不是一个单一的数值，它是关于句子中一个特定位置信息的 d 维的向量。

其次，这种编码没有集成到模型本身上。相反，这个向量用于给每个单词分配一个有关其在句子中位置的信息。换句话说，PE只和输入有关，而和模型无关。

假设​ $t$ 是输入序列的一个位置，​ $\vec{p_t} \in \mathbb{R}^d$ 是它对应的编码，​ $d$ 是维度。定义 $f : \mathbb{N} \rightarrow \mathbb{R}^d$ ​是产生​ $\vec{p_t}$ 的函数，它的形式如下：

$\begin{aligned} \vec{p_t}^{(i)} = f(t)^{(i)} & := \begin{cases} \sin({\omega_k} . t), & \text{if}\ i = 2k \\ \cos({\omega_k} . t), & \text{if}\ i = 2k + 1 \end{cases} \end{aligned}$

这里 $i$ ​ 是向量的index，​ $k$ 的引入是为了区分奇偶。其中：

$\omega_k = \frac{1}{10000^{2k / d}}$ 由函数定义可以推断出，它的频率随着向量维度递减。(三角函数频率、周期、波长相关知识)。它的波长范围是​ $[2\pi, 10000 · 2\pi]$ ，这意味着它可以编码最长为10000的位置，第1和第10001的位置编码重复。（这个10000也是可以改的，比如1000，100000，具体可能要实验看结果。）PE可以表示为一个向量，其中每个频率包含一对正弦和余弦。

$\vec{p_t} = \begin{bmatrix} \sin({\omega_1}.t)\\ \cos({\omega_1}.t)\\ \\ \sin({\omega_2}.t)\\ \cos({\omega_2}.t)\\ \\ \vdots\\ \\ \sin({\omega_{d/2}}.t)\\ \cos({\omega_{d/2}}.t) \end{bmatrix}_{d \times 1}$

现在有两个问题： 1. 这种sines和cosines的组合为什么能够表示位置/顺序？ 假设现在我们想用二进制来表示数字，我们可以观察到不同位置之间的变化率，最后一位在0和1上依次交替，第二低位在每两个数字上交替，以此类推。

$\begin{aligned} 0: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{0}} & & 8: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{0}} \\ 1: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{1}} & & 9: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{1}} \\ 2: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{0}} & & 10: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{0}} \\ 3: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{1}} & & 11: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{1}} \\ 4: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{0}} & & 12: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{0}} \\ 5: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{1}} & & 13: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{1}} \\ 6: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{0}} & & 14: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{0}} \\ 7: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{1}} & & 15: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{1}} \\ \end{aligned}$

但是用二进制表示数字在浮点数空间非常浪费空间，所以可以用它们的对应浮点函数 - 正弦函数。下图展示了一个最多50个单词的句子中的每个单词的位置编码，维度是128。每一行都表示一个位置编码向量。对比上面的二进制数字表示，（每一个数字的二进制对应一个位置编码向量）：横向看，降低它们的频率，从红色的的位变为橙色的位；纵向来看，左侧上下变化较大，越向右上下变化差越小。所以实际上，正弦函数等效于二进制表示。

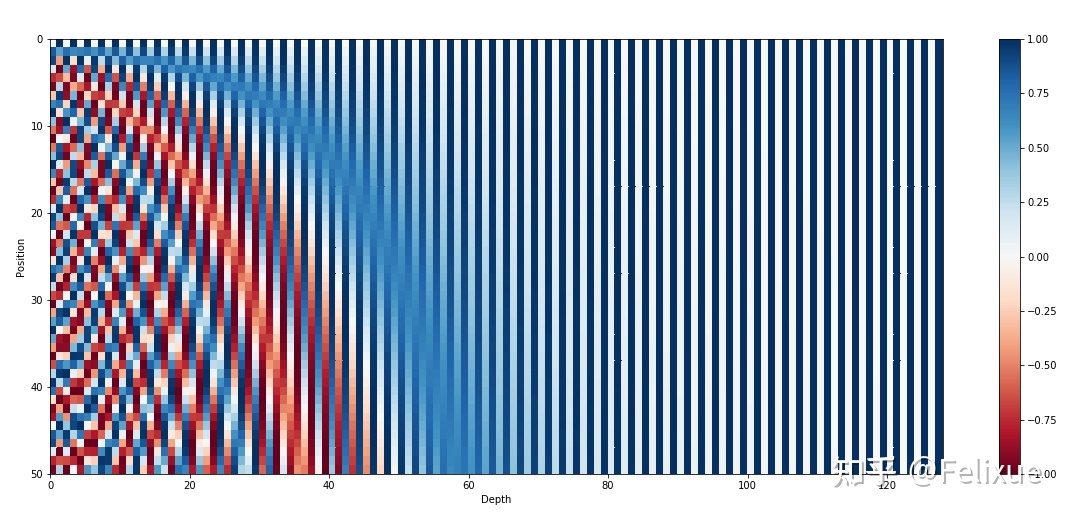
这种正弦曲线位置编码的另一个性质是，相邻时间步的位置编码的距离（点积）是对称的，并且会随着时间很好地衰减。

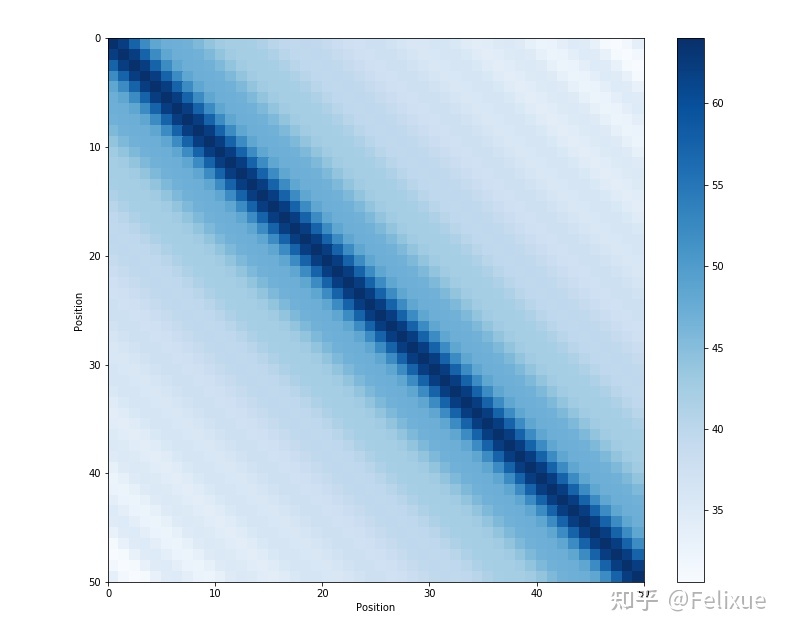
2. 为什么这种正弦曲线形的位置编码可以轻松允许模型获取相对位置relative positioning？ Attention原文是这么写的:

We chose this function because we hypothesized it would allow the model to easily learn to attend by relative positions , since for any fixed offset k, ​ $PE_{pos+k}$ can be represented as a linear function of $PE_{pos}$ ​.

为什么这句话成立？这篇博客给了一个完整的证明。这里放一个中文简要整理版（非严格证明）： 求证： 对于每一对对应频率 $w_k$ ** ​ 的 sine-cosine 对，有一个线性变换矩阵​ ** $M \in \mathbb{R}^{2\times2}$ （独立于 $t$ ​）满足以下等式:

$M.\begin{bmatrix} \sin(\omega_k . t) \\ \cos(\omega_k . t) \end{bmatrix} = \begin{bmatrix} \sin(\omega_k . (t + \phi)) \\ \cos(\omega_k . (t + \phi)) \end{bmatrix}$

证明： 令 ​ $M$ 是一个 ​ $2 \times 2$ 的矩阵，需要找到 ​ $u_1, v_1, u_2, v_2$ 使得：

$\begin{bmatrix} u_1 & v_1 \\ u_2 & v_2 \end{bmatrix} .\begin{bmatrix} \sin(\omega_k . t) \\ \cos(\omega_k . t) \end{bmatrix} = \begin{bmatrix} \sin(\omega_k . (t + \phi)) \\ \cos(\omega_k . (t + \phi)) \end{bmatrix}$

左边矩阵向量相乘，右边运用三角函数和角公式：

$\begin{aligned} u_1 \sin(\omega_k . t) + v_1 \cos(\omega_k . t) = & \ \ \ \ \cos(\omega_k .\phi)\sin(\omega_k . t) + \sin(\omega_k .\phi)\cos(\omega_k . t)\\ u_2 \sin(\omega_k . t) + v_2 \cos(\omega_k . t) = & - \sin(\omega_k . \phi)\sin(\omega_k . t) + \cos(\omega_k .\phi)\cos(\omega_k . t)\end{aligned}$

于是得到：

$\begin{aligned} u_1 = \ \ \ \cos(\omega_k .\phi) & \ \ \ v_1 = \sin(\omega_k .\phi) \\ u_2 = - \sin(\omega_k . \phi) & \ \ \ v_2 = \cos(\omega_k .\phi) \end{aligned}$

即矩阵 $M$ ​ 为：

$M_{\phi,k} = \begin{bmatrix} \cos(\omega_k .\phi) & \sin(\omega_k .\phi) \\ - \sin(\omega_k . \phi) & \cos(\omega_k .\phi) \end{bmatrix}$

证毕。

可以看到 $M$ ​ 并不依赖 ​ $t$ 。这个证明说明我们可以用 $\vec{p_{t}}$ ​ 的线性表达来表达任意 ​ $\phi$ 间隔的 ​ $\vec{p_{t+\phi}}$ 。这种性质，使得模型可以很容易获取相对位置。

--------------------------------------------- 为什么PE和WE (word embeddings)是相加(add)，而不是拼接(concatenate)？ 目前这个问题没有理论证明。（？）但是加法相对于拼接减少了模型的参数量，那么上面的问题换个说法就是“PE直接加到WE上是不是有什么缺点？” 这个不一定 。回到上面的位置编码的可视化图，我们会发现：相对于整个embedding来说，只有前面少数dimension是用来存储位置信息的。由于embedding只有128维，不够明显，借用另一个博客的图：

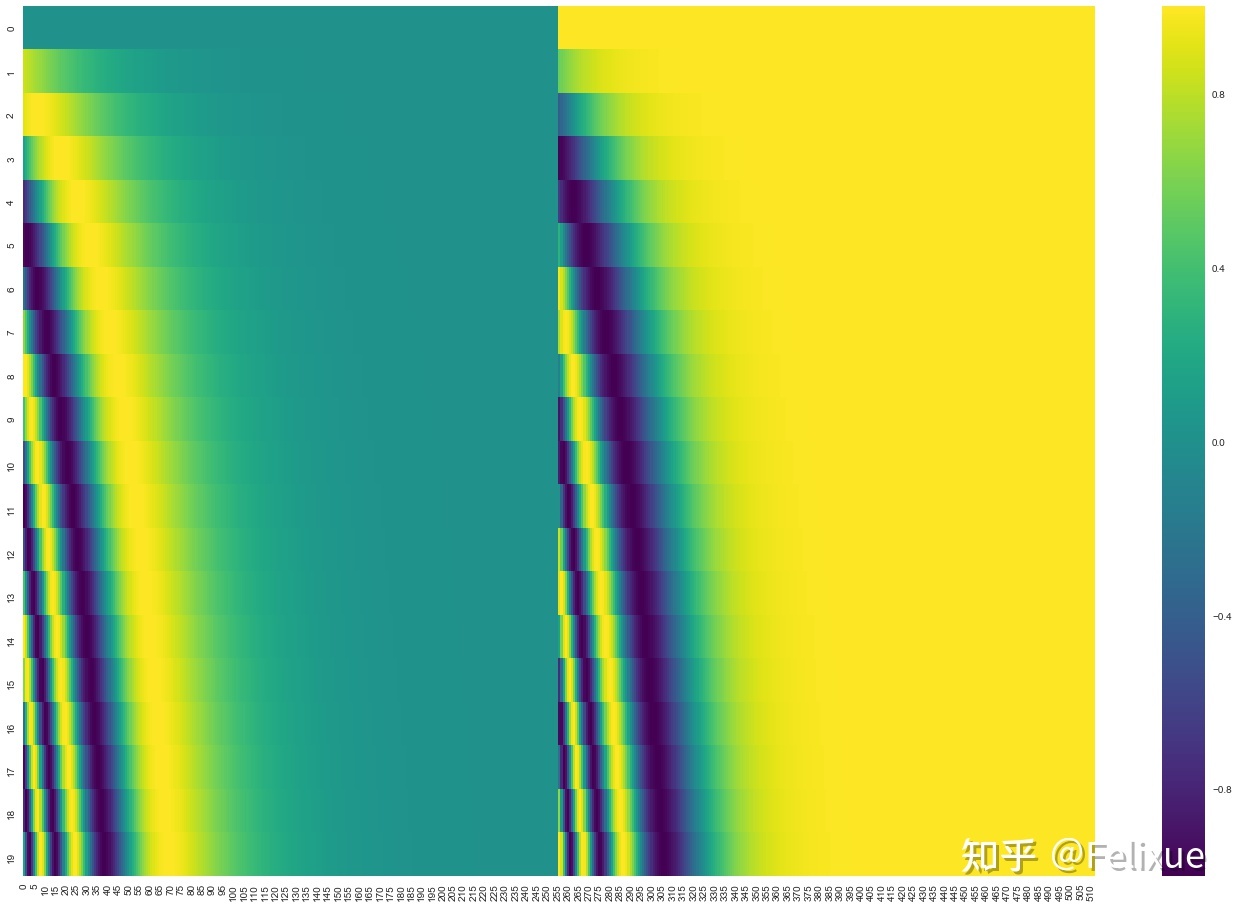
这幅图表示20个单词的512维的位置编码。图中是sine（左）和cosine（右）拼接之前的样子。大部分的维度（全绿/黄）几乎只共享常数1或者-1，换句话说 这些维度都用表示word embedding的信息了 。另外，由于Transformer中PE和WE是从头开始训练的，因此参数的设置方式可能是单词的语义不会存储在前几个维度中，以免干扰位置编码。（这也是这个问题的解： PE是如何训练的？或者说如何让模型知道这些embeddings是position信息？ ）从这个角度来看，Transformer或许可以分离语义信息和位置信息。这样的话，考虑分类PE和WE可能就不会是一个优点了，可能加法提供了额外的可以学习的特征。上面那幅图sine和cosine合起来大概是这样（部分图）：

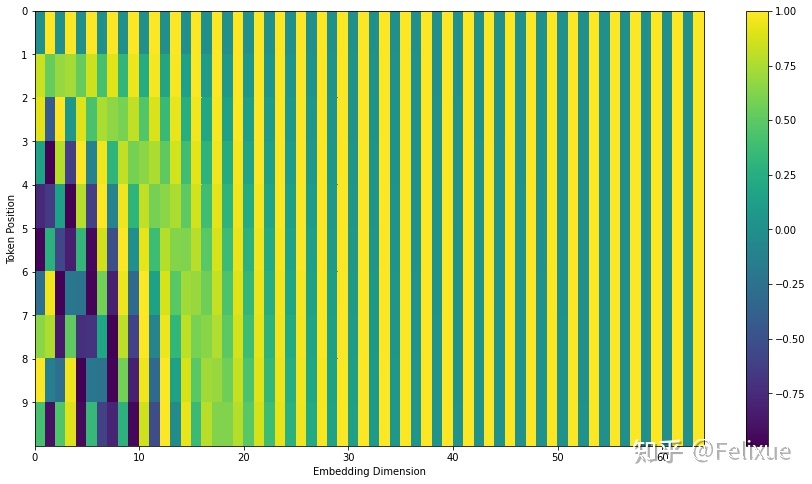
--------------------------------------------- 为什么sine和cosine都被用到了？ 只用它们的组合才能用sin(x)和cos(x)的组合线性表示sin(x+k), cos(x+k)。--------------------------------------------- 固定PE和可学习PE比孰优孰劣？ 目前没有明显的差距，多数论文都会做相关的ablation study。--------------------------------------------- 位置信息到高层后信息会丢失吗？ 不会，因为Transformer结构有残差连接。

---

positional embedding是如何训练的？

reddit 上ID为 pappypapaya 的这个人提出了一个比较有意思的说法，大概意思如下：

在注意力机制中，我们一般输入两个embedding x和y，将 x 经过 Query 转换矩阵 Q，将 y 经过 Key 转换矩阵 K，然后比较Query和Key向量的点积相似度。所以，我们一般需要计算Qx和Ky之间的点积，我们将其写为：

$(Qx)^T (Ky) = x^T(Q^TKy)$

因此，我们只需要等效学习一个联合Query-Key的转换矩阵​ $Q^TK$ ，即可将辅助输入 y​ 转换到一个可以与 x​ 比较的新空间。

通过分别向 ​x 和 y​ 添加位置编码 e​ 和 f​，我们实际上将点积更改为:

$\begin{aligned} (Q(x+e))^{T}(K(y+f)) &= (Qx + Qe)^T(Ky + Kf) \\ &= (Qx)^TKy + (Qx)^TKf + (Qe)^TKy + (Qe)^TKf \\ &= x^T(Q^TKy) + x^T(Q^TKf) + e^T(Q^TKy) + e^T(Q^TKf) \end{aligned}$

原始的 ​ $x^T(Q^TKy)$ 问的是：“ 对于给定的单词 y ​，我们应该对单词 ​x 给予多大的关注 ”。现在多出来三项：

1. $x^T(Q^TKf)$ ： "给定单词 y​ 的位置 f​， 我们应该对单词 x​ 给予多少关注"；
2. $e^T(Q^TKy)$ ： "给定单词 y​ ，我们应该对单词 x​ 的位置 e​ 给予多少关注"；
3. $e^T(Q^TKf)$ ： "给定单词 y​ 的位置 f​， 我们应该对单词 x​的位置e​ 给予多少关注"。

本质上，具有位置编码的学习变换矩阵 $Q^TK$ ​必须同时完成所有这四个任务。这部分可能看起来效率低下，因为从直觉上讲，应该在 ​ $Q^TK$ 同时出色地完成四个任务的能力之间进行权衡。

但是，pappypapaya的猜测是，由于高维满足一些近似正交条件，因此当我们强制 ​ $Q^TK$ 完成所有这四个任务时，实际上并没有权衡取舍。直觉是，在高维中随机选择的矢量几乎总是近似正交的。没有理由认为单词向量和位置编码向量之间有任何关联。如果 word embedding 形成一个较小维的子空间，而 positional embedding 形成另一个较小维的子空间，那么这两个子空间本身可能近似正交，因此可以通过学习得到的 $Q^TK$ ​ 对这些子空间独立进行近似变换（因为它们基本上存在于高维空间中的不同轴上）。不确定这个想法是否正确，但是从直觉上看是可能的。

如果为true，那么可以解释为什么 positional embedding 通过 addition 结合而不是 concatenation 。Concatenation 可以确保 position 维度与 word 维度正交。但猜测，由于这些 embedding 的 size 非常大，因此即使是 addition 也可以免费获得近似的正交性，而不必花费 concatenation​ 的代价（有许多参数需要学）。