3D Gaussian Splatting 用于动态场景表示
# (3DV 2024) Dynamic 3D gaussians: Tracking by persistent dynamic view synthesis
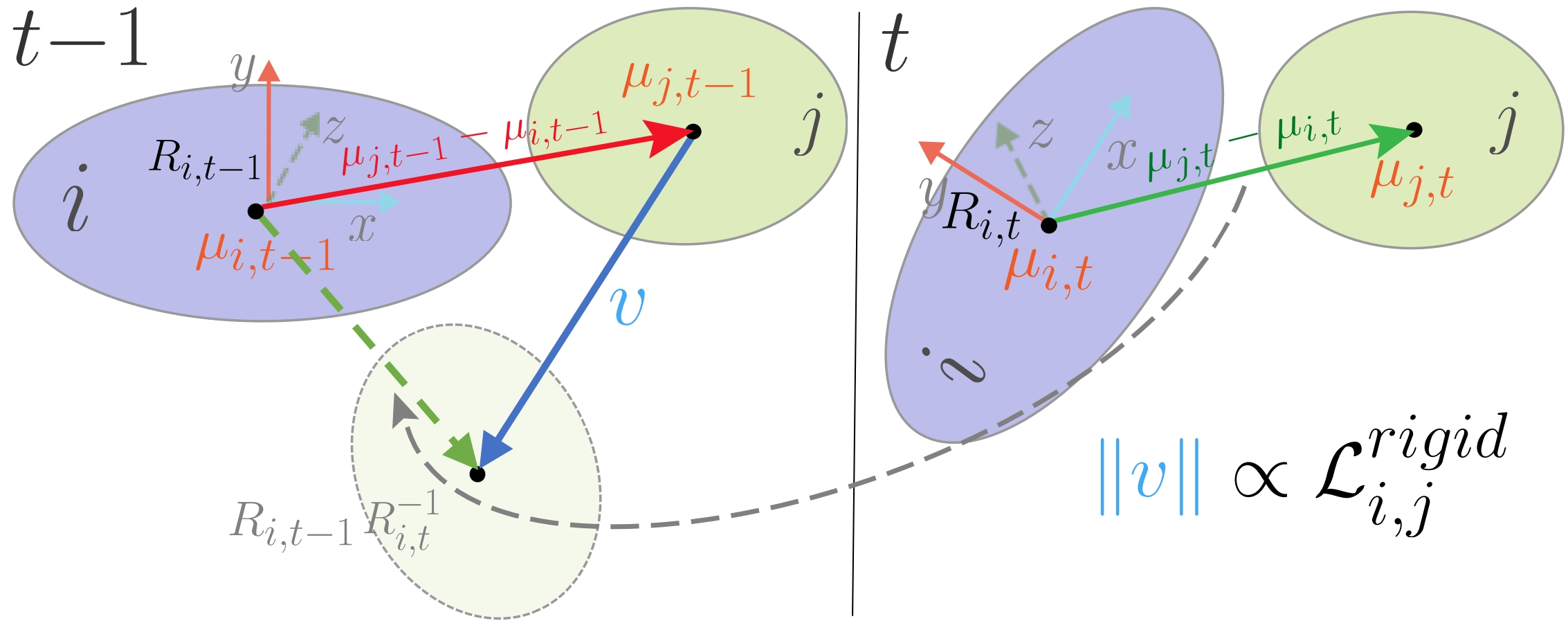
基于物理启发出了三个正则化项加在loss函数里面:
- local-rigidity loss 局部刚度:一个Gaussian绕着某个轴旋转,相近的Gaussian都要跟着绕这个轴转
Li,jrigid=wi,j∥∥∥(μj,t−1−μi,t−1)−Ri,t−1Ri,t−1(μj,t−μi,t)∥∥∥2
Lrigid=k∣S∣1i∈S∑j∈knni;k∑Li,jrigid
- local-rotation similarity 局部旋转相似性:相近的Gaussian相同旋转,作者加它的理由是实验发现效果更好
Lrot=k∣S∣1i∈S∑j∈knni;k∑wi,j∥∥∥q^j,tq^j,t−1−1−q^i,tq^i,t−1−1∥∥∥2
- local-isometry loss 局部等距:相近的Gaussian相对位置不变,作者加它的理由是上面两个loss容易导致撕裂,加它防止撕裂
Liso=k∣S∣1i∈S∑j∈knni;k∑wi,j∣∣∣∥μj,0−μi,0∥2−∥μj,t−μi,t∥2∣∣∣
其中,这里的“相近的Gaussian”是用K-nearst给每个Gaussian找20个点,并将其距离作为算上述正则化项的权值:
wi,j=exp(−λw∥μj,0−μi,0∥22)
# (ICLR 2024) Real-time Photorealistic Dynamic Scene Representation and Rendering with 4D Gaussian Splatting
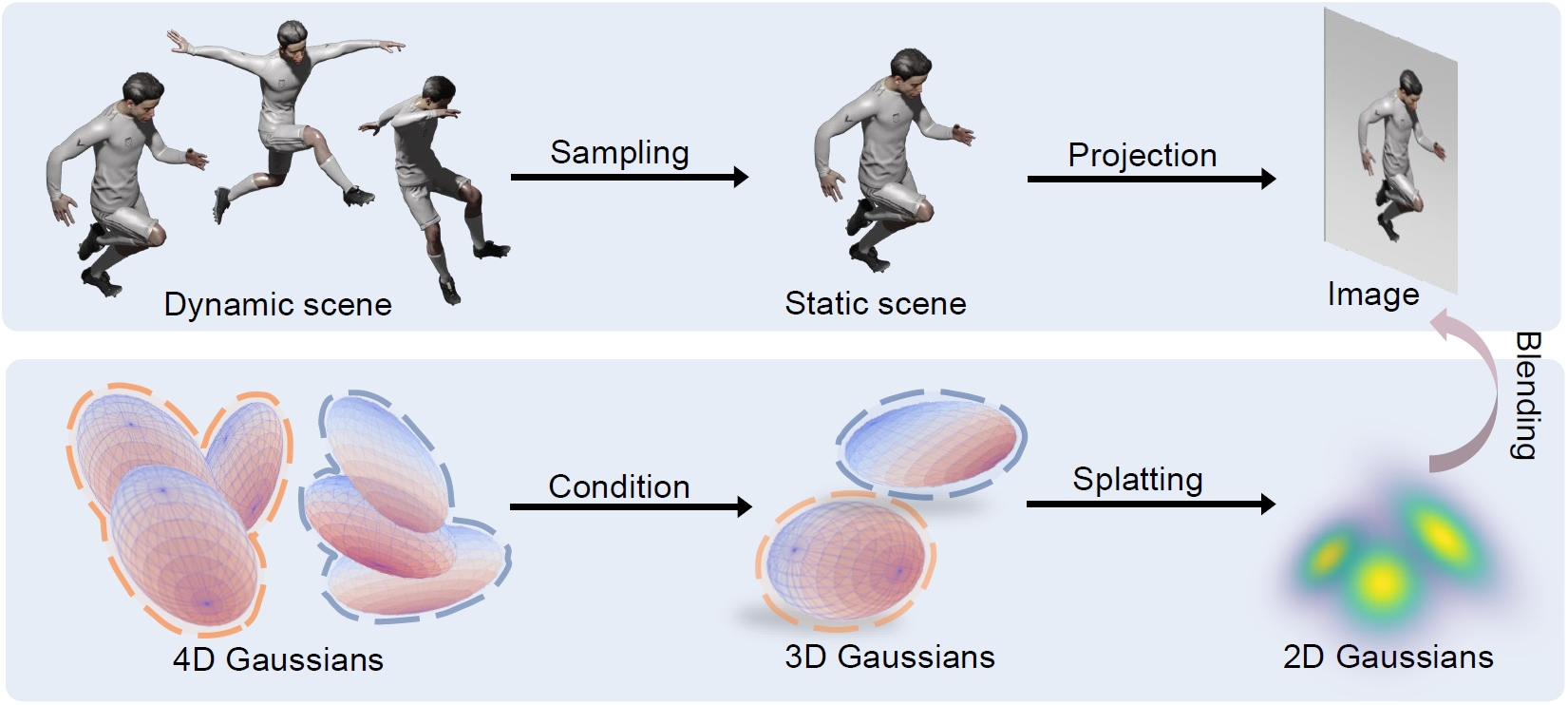
3D Gaussian形状参数里的位置、rotate和scale都变成4D,相当于3D Gaussian(椭圆)加一个时间维度变成了4D椭圆,渲染是在时间轴上采样从而将这个4D椭圆投影到3D空间。
文中介绍的3D Gaussian:

拓展到4D Gaussian:

缩放3D变4D在数学上是3x3对角矩阵变成4x4对角矩阵S;旋转3D变4D在数学上是两个啥矩阵相乘得到R; 从而4D Gaussian均值(中心点坐标)变成4维μ、协方差也变成4x4矩阵Σ:

最后,每个时刻的3D Gaussian是从这个4D Gaussian中采样而来(4D椭圆于t时刻在3D空间中的一个投影):

球谐系数加上一个维度用傅里叶级数组成的函数表示:

# 4D Gaussian Splatting for Real-Time Dynamic Scene Rendering
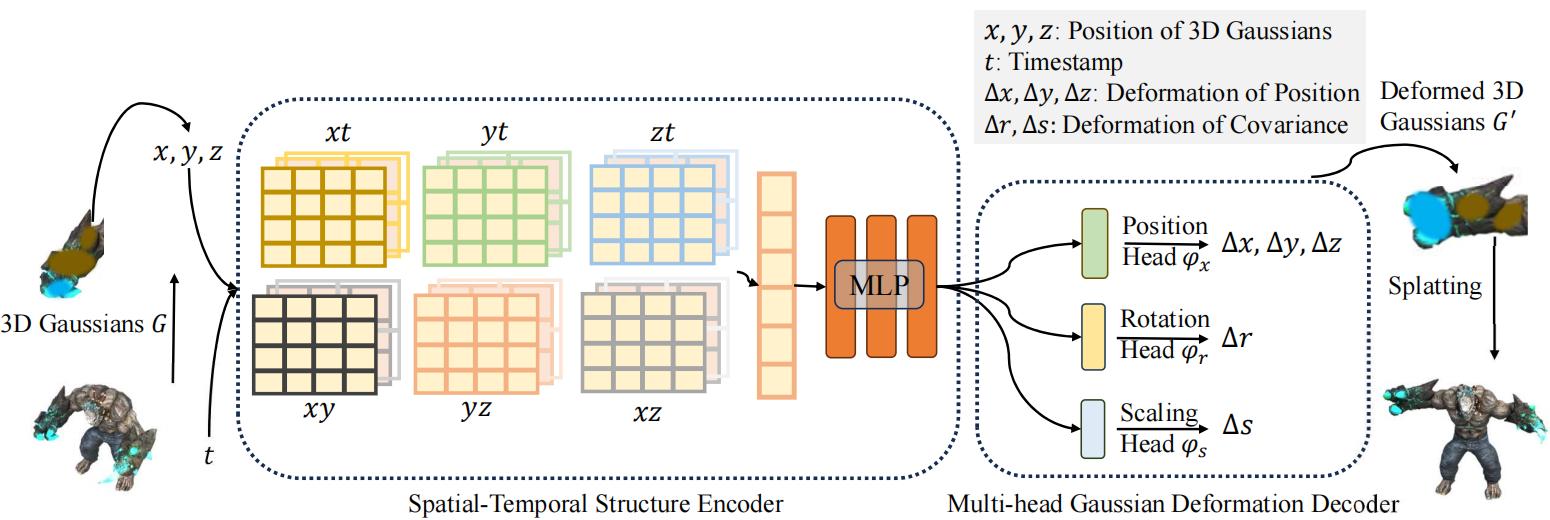
高斯点云只有一个,用Triplane存储运动信息。
任意高斯点位置xyz和时间t输入Triplane得到位移/旋转/缩放的变化情况,从而对高斯点进行变换。
(只有形状方面的变换,没有颜色和球谐系数的变化)
