图灵机

图灵机(Turing Machine, TM)在自动机领域也只是大大小小机器中的一个，但因其与可计算函数的等价性使得它成为自动机领域一类比较特殊的机器。

# 确定的图灵机的形式化定义

$M=(Q,\Sigma,\Gamma,\delta,q_0,B,F)$

$Q$ ：有穷状态集
$\Sigma$ ：字母表（有穷输入符号集）
$\Gamma$ ：所有可以放置在输入字符串中的字符（有穷带符号集）， $\Sigma\subseteq\Gamma$ 包含字母表和空格符号
$\delta$ ：状态转移函数， $\delta:Q\times\Gamma\rightarrow Q\times\Gamma\times\{L,R\}$
$q_0$ ：初始状态， $q_0\in Q$
$B$ ：空格符号， $B\in\Gamma-\Sigma$
$F$ ：终结状态集（接受状态集）， $F\subseteq Q$

状态转移函数 $\delta$ 表示当前状态和输入符号的笛卡尔积到下一个状态、写入符号和移动方向的映射；它的输入是当前状态+字符串中的一个符号，输出下一个状态+要将字符串中的当前符号改变为什么符号+接下来读取该字符左边还是右边的字符（不能停止不动，字符串向左向右都是无限长）。

当图灵机到达 $F$ 中的某个状态时结束。

例如 $(q_1,Y,L)=\delta(q_0,X)$ 表示当前状态为 $q_0$ 、当前读取的字符为 $X$ ，然后图灵机的状态改变为 $q_1$ 、将当前字符修改为 $Y$ 、接下来读取左边的字符（“ $L$ ”）。在状态转移图中表示为：

# 确定的图灵机的瞬时描述(Instantaneous Description, ID)

图灵机的输入虽然是有限长，在有限步内所到达的字符串的非空内容总是有限的，因此可以使用字符串和状态 $q$ 以及 $q$ 在字符串上的位置定义图灵机的瞬时描述：

$X_1X_2...X_{i-1}qX_iX_{i+1}...X_n$

$q$ 为图灵机的当前状态
$i$ 为图灵机当前读取的位置
$X_i,i\in[1,n]$ 为图灵机在有限步内所到达的字符串的非空内容

# ID转移： $\vdash$

在图灵机 $M$ 中， $(q_1,Y,L)=\delta(q_0,X)$ 的ID转移表示为：

$X_1X_2...X_{i-1}q_0X_iX_{i+1}...X_n\vdash_MX_1X_2...X_{i-2}q_1X_{i-1}YX_{i+1}...X_n$

在图灵机 $M$ 中， $(q_1,Y,R)=\delta(q_0,X)$ 的ID转移表示为：

$X_1X_2...X_{i-1}q_0X_iX_{i+1}...X_n\vdash_MX_1X_2...X_{i-1}Yq_1X_{i+1}X_{i+2}...X_n$

若某ID $I_1$ 是由另一个ID $I_0$ 经过有限步（包括0步）转移得到的，则记为 $I_0\vdash_M^*I_1$ 。

# 图灵机的语言

某个图灵机定义为 $M=(Q,\Sigma,\Gamma,\delta,q_0,B,F)$ ，则所有的可以让 $M$ 通过有限步ID转移到接受状态的字符串的集合，称为图灵机 $M$ 的语言：

$\bm L(M)=\{w\in\Sigma^*|(\exist p\in F,\alpha\in\Gamma^*,\beta\in\Gamma^*)q_0w\vdash_M^*\alpha p\beta\}$

递归可枚举语言/图灵可识别语言： $L=\bm L(M)$
递归语言/可判定语言： $L=\bm L(M)\wedge(\forall w\in\Gamma^*)\text{M能停机}$

注：图灵机不保证对所有字符串输入都停机。保证停机的图灵机在实际应用中是算法的好模型，是算法概念的形式化。

# 图灵机变种

以下的图灵机都可证明与确定的图灵机等价，但可以让图灵机的设计更加简单。

# 可以存储有限个符号的图灵机

$M=(Q',\Sigma,\Gamma,\delta,q_0',B,F)$

$Q'=Q\times\Gamma\times...\times\Gamma$ ：图灵机的状态是由一个状态和多个符号组成的序列（元组）
$q_0'=[q_0,B,...,B]$ ：图灵机的初始状态由一个状态和多个空白符组成

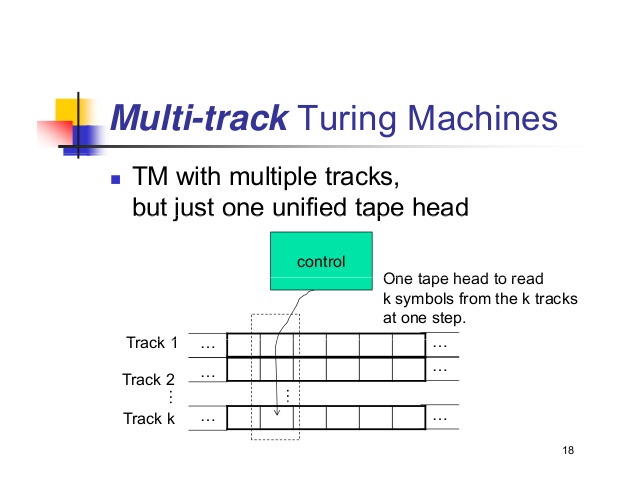
# 多道图灵机

$M=(Q,\Sigma,\Gamma',\delta,q_0,B',F)$

$\Gamma'=\Gamma\times\Gamma\times...\times\Gamma$ ：图灵机的输入不是一个字符串而是一个固定长度的字符元组串

多道图灵机

# 半无穷带图灵机

字符串输入只有一侧是无穷的

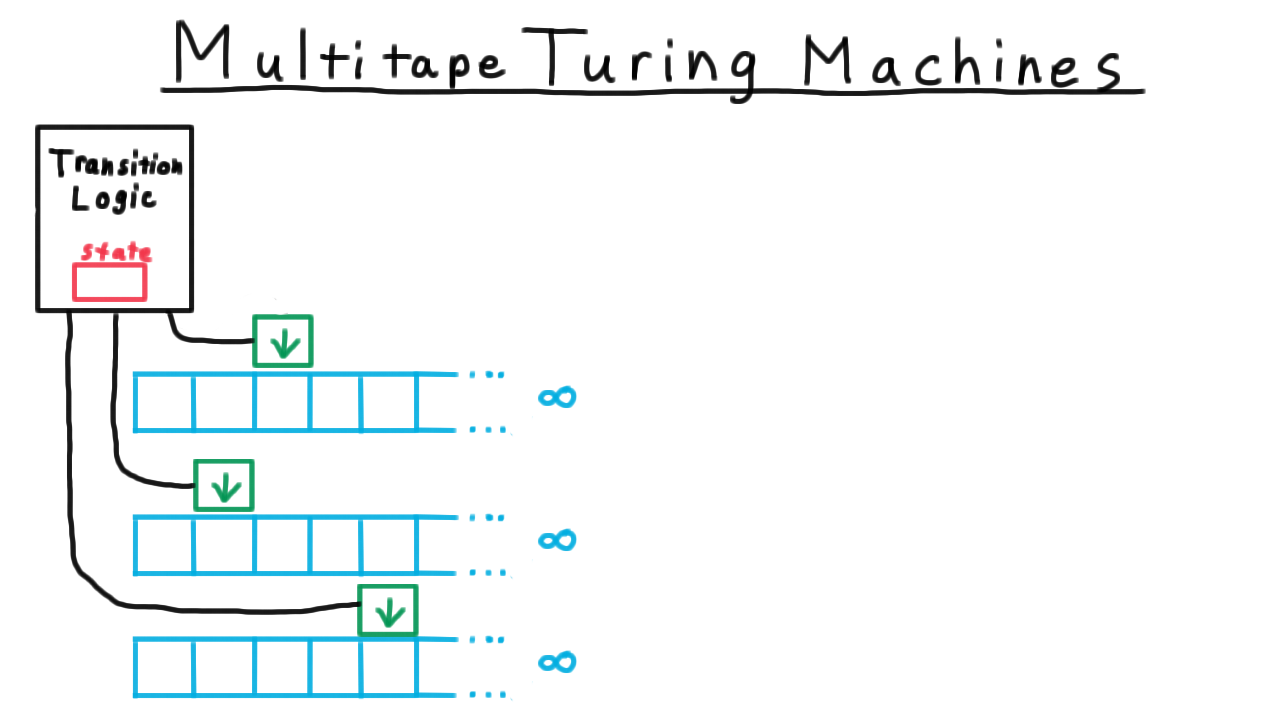
# 多带图灵机

字符串输入有多个
图灵机在每个字符串上可以处于不同的位置
图灵机在每个字符串上的位置移动相互独立
图灵机在字符串上的移动除向左向右外，还可以是停止状态

多带图灵机

# 非确定的图灵机(Nondeterministic Turing Machine, NTM)

$M=(Q,\Sigma,\Gamma,\delta,q_0,B,F)$

$\delta$ $δ$ ：状态转移函数， $\delta:Q\times\Gamma\rightarrow 2^{Q\times\Gamma\times\{L,R\}}$ $δ : Q \times Γ \to 2^{Q \times Γ \times {L, R}}$
- 类比NDA，NTM的状态转移函数输出为TM状态转移函数输出元组的集合，表示当前所有可能的状态转移过程

# 计算复杂性引入

运行时间：图灵机在某个输入上停机前移动的步数
时间复杂度 $T(n)$ ：图灵机 $M$ 在所有长度为 $n$ 的输入上的运行时间的最大值。
只有保证停机的图灵机 $T(n)$ 才有意义
只有多项式时间的 $T(n)$ 才能在实际的计算机上可解

上面这些图灵机变种都与确定的图灵机等价，它们都能用来模拟确定的图灵机（显然），也都能被确定的图灵机所模拟。接下来看看如何模拟并分析一下模拟的时间复杂度。

# 用确定的图灵机模拟可以存储有限个符号的图灵机

显然，令确定的图灵机的状态集合为可以存储有限个符号的图灵机的所有可能的状态和存储符号的组合即可。模拟移动 $n$ 步的时间复杂度为 $O(n)$ 。

# 用确定的图灵机模拟多道图灵机

显然，令确定的图灵机的输入为字符元组就是一个多道图灵机了。模拟移动 $n$ 步的时间复杂度为 $O(n)$ 。

# 用确定的图灵机模拟可以存储有限个符号的多道图灵机

显然，令确定的图灵机的状态集合为可以存储有限个符号的图灵机的所有可能的状态和存储符号的组合，并令其输入为字符元组即可。模拟移动 $n$ 步的时间复杂度为 $O(n)$ 。

# 用可以存储有限个符号的多道图灵机模拟多带图灵机

思路：对于 $k$ 带图灵机，用 $2k$ 道图灵机模拟之。对于每个带，都用两个道模拟，一个道存带的内容，一个道存图灵机在当前带的位置。

从左到右扫描一次，存储图灵机在所有带的位置和对应位置的输入
执行状态转移函数，存储图灵机在所有带的移动状态和要修改动作
从右到左扫描一次，按照移动状态修改道上的位置记录、按照修改动作修改道上的数据
重复1~3直到可接受状态

模拟移动1步需要左右扫描一次，时间复杂度 $O(n)$ ，因此模拟移动 $n$ 步的时间复杂度为 $O(n^2)$ 。

# 用多带图灵机 $M$ 模拟NTM $N$ ：广度优先搜索

思路：同NDA一样，NTM的运行过程也可以看作是树，其节点是ID，分支是由于NTM选择了多个状态转移而产生多个ID转移进而产生多个ID。若要用“串行”的图灵机模拟之，则可考虑对NTM运行时树上的ID进行广度优先搜索。

$M$ 有两条带，第一条带保存 $N$ 中产生而未处理的ID，第二条带用于对ID进行处理。

把第一条带开头的ID复制到第二条带
若第二条带上的ID可接受则停止
否则将第二条带上的可能的ID转移复制到第一条带的末端
抹去第二条带开头的ID
重复1~4

模拟每个ID都要读取复制和删除长度为 $n$ 的ID，时间复杂度 $O(n)$ ，若每一个ID至多产生 $m$ 个选择，那经过 $n$ 步要模拟 $\sum_{i=1}^nm^i=\frac{m^{n+1}-1}{m-1}$ 个ID，总的时间复杂度为 $O(nm^n)$ 。

# $P=NP$ 问题

前面分析出来了用NTM能用多带图灵机进行模拟，但模拟需要指数时间，但这只是一种最直观的模拟方法，是否存在多项式时间的模拟方法？目前还是未知的。

这个问题可以概括为：NTM以多项式时间解决的问题，TM是否也可以以多项式时间解决？

简称 $P=NP$ 问题。其中

$P$ 表示“Polynomial”——“多项式”，指确定的图灵机在多项式时间内可以解决的问题的问题类
$NP$ 表示“Non-Deterministic Polynomial”——“非确定的多项式”，指非确定的图灵机在多项式时间内可以解决的问题的问题类
“ $NP$ 完全”表示任何NP问题都可以在多项式时间内规约到这个问题

虽然问题目前还没解决，但是实际应用中通常认为 $P\not ={NP}$ 。

# 图灵机的二进制表示

显然，由 $0$ 和 $1$ 组成的字符串可以编码任何的字符系统，因此所有的图灵机都可以编码为 $\Sigma=\{0,1\}$ 上的图灵机。

# 对 $\Sigma^\ast=(\bm 0+\bm 1)^\ast$ 中的字符串编码

将 $(\bm 0+\bm 1)^*$ 按长度和字典序进行排序，可以发现第 $i$ 个串 $w_i$ 开头加1就是 $i$ 的二进制表示：

$(i)_2=1w_i$

因此可以构造如下编码

$i$	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$\dots$
$(i)_2$	$1\varepsilon$	$10$	$11$	$100$	$101$	$110$	$111$	$\dots$
$w_i$	$\varepsilon$	$0$	$1$	$00$	$01$	$10$	$11$	$\dots$

# 对图灵机的状态转移函数编码

令 $Q=\{q_1,q_2,\dots,q_{|Q|}\}$ $Q = {q_{1}, q_{2}, \dots, q_{∣ Q ∣}}$ ，从而每一个状态可以由一个数字表示
- 开始状态为 $q_1$ ，终止状态为 $q_2$
令 $\Gamma=\{X_1,X_2,\dots,X_{|\Gamma|}\}$ ，从而输入字符串的每一个符号可以由一个数字表示
令移动方向 $L=D_1$ 、 $R=D_2$ ，从而移动方向可以由一个数字表示

因此，图灵机的每一个状态、输入符号和移动方向都可以由一个数字表示，进而根据 $01$ 字符串的编码规则，它们也都可以由 $(\bm 0+\bm 1)^*$ 中的字符串表示。

由于图灵机的状态转移函数 $\delta:Q\times\Gamma\rightarrow 2^{Q\times\Gamma\times\{L,R\}}$ 是离散的，因此可以被表示为一系列状态转移规则的集合：

$\Delta=\left\{(q,X)\rightarrow(q',X',D)|q,q'\in Q\wedge X,X'\in\Gamma\wedge D\in\{L,R\}\right\}$

在此定义下的状态转移函数则表示为：

$\delta(q,X)=(q',X',D)\quad(q,X)\rightarrow(q',X',D)\in\Delta$

而根据上述编码规则，任何一个转移规则 $(q_i,X_j)\rightarrow(q_k,X_l,D_m)\in\Delta$ 都可以用一个五元组 $(i,j,k,l,m)$ 唯一表示。因此，我们可以将状态转移规则编码为5个由字符 $0$ 构成的字符串，中间以字符 $1$ 分隔：

$C=0^i10^j10^k10^l10^m\quad\delta(q_i,X_j)=(q_k,X_l,D_m)$

# 对图灵机编码

根据上面的分析可以看出，所有的图灵机的状态、输入符号和移动方向都可以由相同的编码方式表示，不同的图灵机本质上只在转移规则上有所不同，因此对一个图灵机的编码就是对其转移规则的编码。

因此，根据上述对图灵机的状态转移函数编码规则，我们可以将图灵机编码为一个由状态转移规则的编码组成的字符串，中间用两个字符 $1$ 分隔：

$C_111C_211C_311\dots C_{n-1}11C_n$

即得到图灵机编码，也即图灵机的二进制表示。

进而根据对 $\Sigma^*=(\bm 0+\bm 1)^*$ 中的字符串编码规则，我们又可以将图灵机的编码对应到一个数字 $i$ ，进而又可以定义“第 $i$ 个图灵机” $M_i$ ：

$\text{图灵机}M_i:=\text{编码为}w_i\text{的图灵机}$

# 通用图灵机

# 对角化语言 $L_d$

对角化语言是所有不能接受自身编码的图灵机的编码组成的集合：

$L_d=\{w_i|w_i\not\in\bm L(M_i)\}$

注： $L_d$ 为什么叫做“对角化”？把编码按顺序排成一张表，行为图灵机，列为编码字符串，表内容为“接受”或“拒绝”， $L_d$ 就是对角线上的内容为“接受”的格所对应的列。

图灵机 $\rightarrow$
字符串 $\downarrow$	$M_1$	$M_2$	$M_3$	$M_4$	$M_5$	$\dots$
$w_1$	拒绝	拒绝	接受	接受	拒绝
$w_2$	接受	拒绝	拒绝	接受	拒绝
$w_3$	拒绝	接受	接受	拒绝	拒绝
$w_4$	拒绝	拒绝	接受	接受	接受
$w_5$	接受	接受	拒绝	拒绝	拒绝
$\vdots$

# 证明对角化语言不是图灵可识别语言（不存在识别它的图灵机）

假设有一个图灵机 $M_i$ 识别对角化语言：

$L_d=\bm L(M_i)$

那么有对于它的编码 $w_i$ ：

$\begin{aligned} &w_i\in L_d\\ \Leftrightarrow&w_i\in\{w_i|w_i\not\in\bm L(M_i)\}&L_d\text{的定义}\\ \Leftrightarrow&w_i\not\in\bm L(M_i)&L_d\text{的定义}\\ \Leftrightarrow&w_i\not\in L_d&L_d=\bm L(M_i)\\ \Rightarrow&\text{矛盾}\\ \end{aligned}$

因此识别对角化语言的图灵机不存在，故对角化语言不是递归可枚举语言。

# 通用语言 $L_u$

根据上文所属的编码方式，我们可以将图灵机 $M_i$ 的编码 $w_i$ 和这个图灵机接受的某个输入串 $w\in\Gamma^*$ 的编码组成一个字符串，中间以三个字符 $1$ 进行分隔：

$w_i111w$

进而构造一种“通用语言”：

$L_u=\{w_i111w|w\in L(M_i)\wedge i\in\mathbb N\}$

# 证明通用语言是图灵可识别语言（通用图灵机 $U$ ）

可以构造一个多带图灵机 $U$ ，当输入 $w_i111w\in L_u$ 时：

读取 $w_i$ 写到第一条带上
读取 $w$ 写到第二条带上
第三条带存储 $M_i$ 的状态

从而模拟图灵机 $M_i$ 在 $w$ 上的活动。进而 $w\in\bm L(M_i)\Rightarrow w_i111w\in\bm L(U)\Rightarrow L_u=\bm L(U)$ 。因此通用语言是图灵可识别语言。

这里的 $U$ 被称为“通用图灵机”，是现代计算机的理论基础。 $U$ 的编码是可以写出来的，罗杰 · 彭罗斯在《皇帝的新脑》中就给出过一个 $U=M_i$ 的十进制 $i$ 值，一共有1654位。

# 证明通用语言不是可判定语言（不能保证所有输入全部停机）

我们可以用通用语言 $L_u$ 的编码方式表示 $L_d$ ，它显然是 $L_u$ 的子集：

$L_{du}=\{w_i111w_i|w_i\not\in\bm L(M_i)\}\subset L_u$

进而：

$\begin{aligned} &L_u\text{是可判定语言}&\\ \Leftrightarrow&U\text{在}L_u\text{上保证停机}&\text{可判定语言定义}\\ \Rightarrow&U\text{在}L_{du}\text{上保证停机}&L_{du}\subset L_u\\ \Leftrightarrow&U\text{可识别}L_d&L_{du}\text{和}L_u\text{等价}\\ \Rightarrow&L_d\text{是图灵可识别语言}&\text{图灵可识别语言定义}\\ \Rightarrow&\text{矛盾}&L_d\text{不是图灵可识别语言} \end{aligned}$

因此通用语言不是可判定语言。这个定理也告诉我们图灵停机问题是不可判定问题。

# 图灵完备性

能模拟上述通用图灵机 $U$ 运行的系统就被称为图灵完备系统，这一定义也等效于能模拟任意图灵机运行的系统。

# 图灵机在数论中的应用：“忙碌的河狸”

原文：《用跑得最慢的电脑程序，理解最高深的哥德巴赫猜想》

# 限制 $|\Delta|$ 的图灵停机问题

尽管前文已经证明图灵停机问题是不可判定的，但我们仍然可以在一定范围内解决图灵停机问题，即问：

“有 $n$ 条状态转移规则的图灵机是否能保证在所有输入上停机？”

按照前面对图灵机编码的讨论可以看出，如果指定了 $n$ 的数量， $|\Delta|=n$ 图灵机的数量就是有限的。因此，我们总可以写下 $|\Delta|=n$ 的所有图灵机，然后一个个判断其是否在所有输入上停机。

由于图灵停机问题的不可判定性，我们必然找不到一个通用的算法判定 $|\Delta|=n$ 的所有图灵机都是否能停机。这意味着对于每个图灵机我们都要单独寻找一个判断方法。这个过程很难，但它至少是可以被计算的。

# “忙碌的河狸”：限制 $|\Delta|$ 的图灵机最大停机步数问题

有了前文有限范围内的图灵停机问题，我们就可以进一步地提出被称为 “忙碌的河狸” 的问题：

“有 $n$ 条状态转移规则的可停机图灵机在停机前最多能走多少步？”

通常，我们将这个步数记为“忙碌河狸数” $BB(n)$

要证明 $BB(2) = 6$ 和 $BB(3) = 107$ 就已经非常复杂了，拉多的学生 Shen Lin 做出了这个成果，并于1965年获得了博士学位。拉多认为， $BB(4)$ 的问题是“彻底的绝望“，不过还是有人在1983年解决了这个问题。除此之外，研究人员对于5条规则的情况，已经找到了一种图灵机，它在运行47176870步之后停机，也就是说， $BB(5)$ 起码比这个数字要大。而 $BB(6)$ 最小也得有 $7.4 × 10^36534$ 。亚伦森说：“除非能找到新观点新思路，否则这个问题根本不可能得到解决。”

——《用跑得最慢的电脑程序，理解最高深的哥德巴赫猜想》

# 不可知的阈值

比方说哥德巴赫猜想，说的是对于任何大于 $2$ 的偶数，总能分解为两个质数的和。要是这个问题能得到解决，那么数论这一学科将迎来史诗般的一刻，数学家对质数分布的了解也会更加深入。2015年，一位网名为Code Golf Addict的Github用户发布了一台27条规则的图灵机代码。这台图灵机非常特别，它当且仅当哥德巴赫猜想不成立时，才会停机。其实很简单，它一开始工作，就会从 $4$ 开始，挨着检查哥德巴赫猜想（当然也是靠遍历）。如果找到了所需的两个质数，就往上继续，以此往复。如果发现了不能表示为质数和的偶数，就会停机。

这种暴力的方法是不可能解决哥德巴赫猜想的，因为如果不停机，我们永远也不会知道猜想是不是正确的。不过，“忙碌河狸”问题为我们提供了一些思路。假如我们能计算出 $BB(27)$ ，那我们最多也只需运行 $BB(27)$ 这么多步，再往上如果还没停机的话，就说明哥德巴赫猜想成立。毕竟 $BB(27)$ 就是27规则停机问题的最大步数了。如果在此之前就停机，自然说明猜想不成立。

困难在于， $BB(27)$ 是如此大的一个数，写下来都很难，要运行那么多次去检验哥德巴赫猜想，这在我们的宇宙中是远不可能的。虽然如此，那个巨大的数字仍然是一个具体的数，亚伦森称，这代表着我们对于数论领域“现有知识的陈述”。

——《用跑得最慢的电脑程序，理解最高深的哥德巴赫猜想》

# 图灵机为何特殊：图灵机和可计算函数

# 可计算函数

$f:\Sigma^*\rightarrow\Sigma^*\text{是一个可计算函数}:=(\exist\text{图灵机}M_i)(\forall\text{合法输入}w)M_i\text{在}w\text{上停机}\wedge\text{停机时输入字符串变为}f(w)$

可计算函数是可计算性理论研究的基本对象。

Yin的笔记本

图灵机